NeuBlog – Motion experiments

Motion experiments

23/07/2025

 

The following set enables to perform motion experiments which incorporate mathematical concepts, allowing for different levels of engagement.

 

Teachers can choose to focus on a qualitative approach, explaining the observed phenomena, or delve deeper into the mathematics to explore the equations and relationships in greater detail. The idea is to feel that mathematics is the language of science.

 

BLT-202 USB/Bluetooth communication module
NUL-213 Motion logger sensor

 

The lesson plan Motion parameters of a moving cart, explores displacement, velocity, acceleration – and understanding their interrelationships.

The lesson plan Newton second Law and the following video, Investigates the relationship between force, mass and acceleration, and analyzes motion through mathematical equations.

 

Newton Second Law experiment video

 

The lesson plan Cart motion on inclined plane, covers the four kinematics equations of motion, studying the behavior of a cart on an incline, and understanding motion with constant acceleration.

All the above lesson plans can be found in Physics experiment page.

The experiment video above can be found in Experiment videos page.

 

Motion parameters

The three main motion parameters are:

  1. Distance (S): Represents how far an object moves from its starting point.
  2. Velocity (V): The rate of change in distance over time, calculated as:
V =
ΔS
Δt
V(average) =
S(final) − S(initial)
t(final) − t(initial)
  1. Acceleration (a): The rate of change in velocity over time, calculated as:
a =
ΔV
Δt
a(average) =
V(final) − V(initial)
t(final) − t(initial)

 

The formula above describes average acceleration (or constant acceleration).
To calculate the object's momentary acceleration (a(t)), we use the ratio of a very small section of velocity change to the corresponding time difference.

 

In Motion parameters of a moving cart experiment, a cart is accelerated forth and back on a track, and we observe and analyze how its distance, velocity and acceleration change over time. The following formulas describe velocity and distance of the accelerated cart as functions of time:

 

Velocity:

V = at + V0

Distance:

S = at2 /2+V0t + S0

Where:

  • V0 = Initial velocity of the cart.
  • S0 = Initial distance from the reference point.
  • a = Acceleration of the cart.
  • t = Time elapsed
Newton second Law

 

Newton second Law experiment deals with Newton's second law of motion that defines the precise relationship between force, mass and acceleration. The law states that the acceleration of an object is directly proportional to the net force applied and inversely proportional to its mass:

F = m ∙ a

Understanding this relationship is crucial in physics and engineering, as it explains the fundamental mechanics behind motion and force interactions.

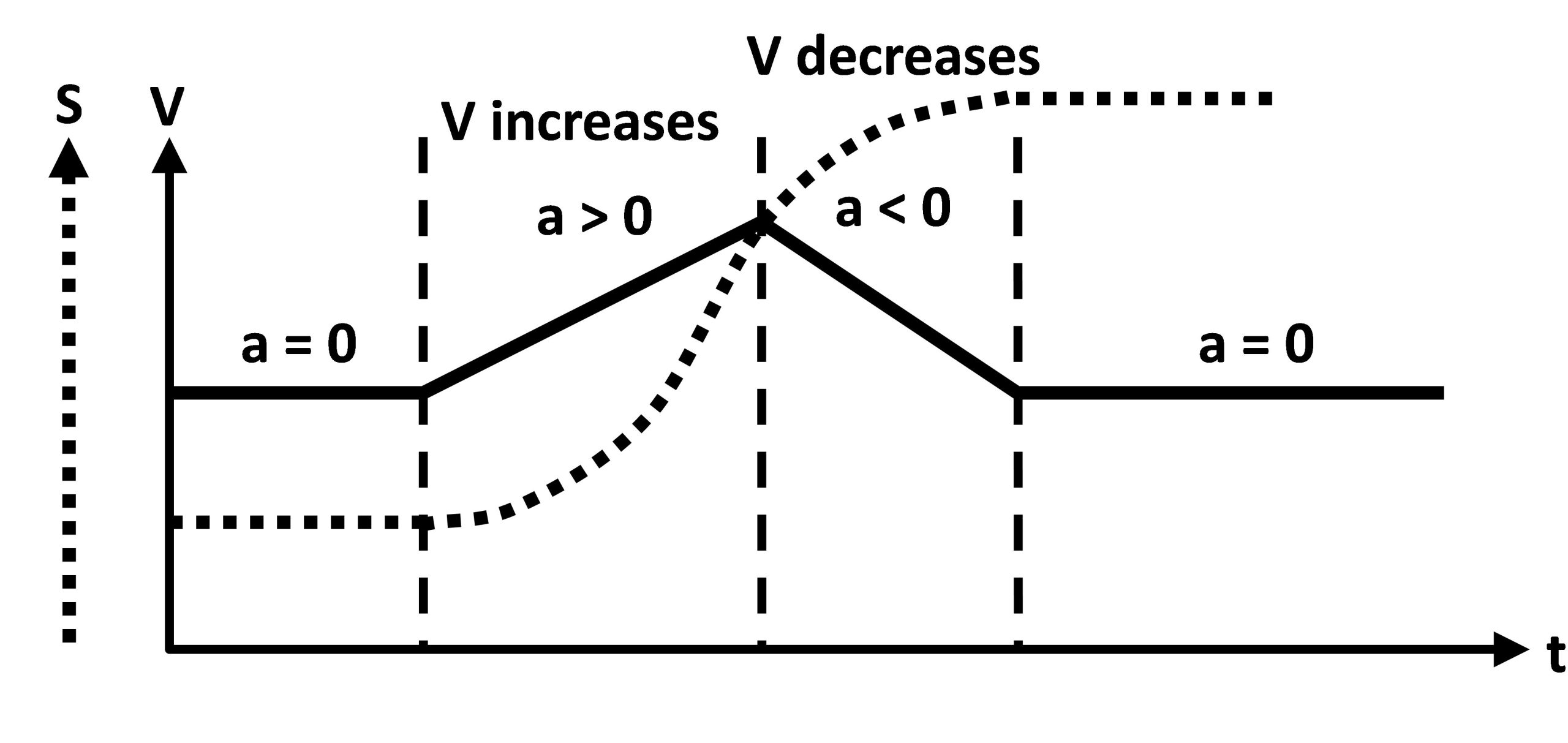
The cart is pulled by a weight and accelerates on a track half of the way and then, decelerates because of the friction.

 

The following graph illustrates the velocity of a cart moving along a track.

velocity of a cart moving along a track

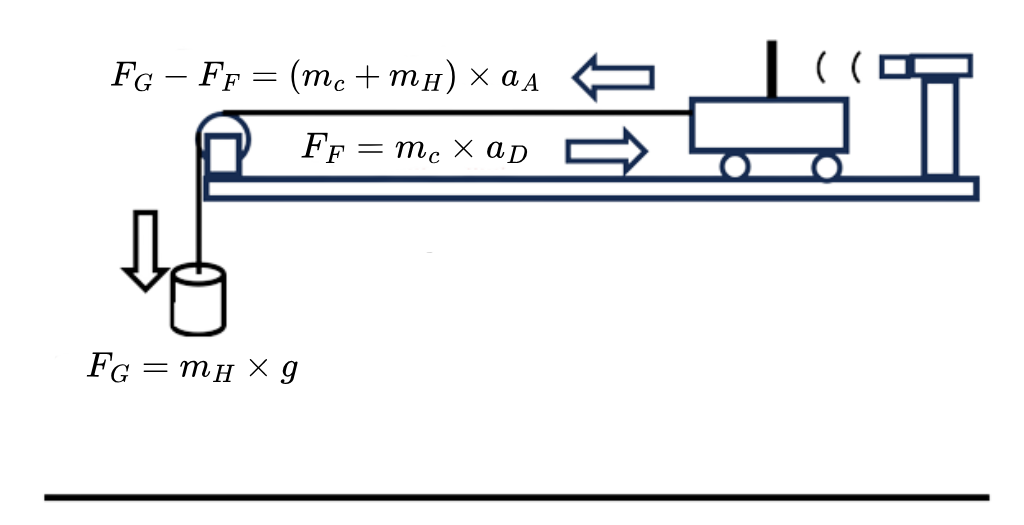
The following picture illustrates the forces acting on the cart.

forces acting on Newton cart

 

In this experiment we learn how to extract the acceleration and the deceleration coefficients from the motion graph.

Motion is described using four fundamental parameters: displacement, velocity, acceleration and time. The kinematic equations allow us to predict unknown motion parameters if others are given. These equations apply only when acceleration remains constant, a condition known as linear motion.

 

Kinematic Equations

In linear motion, velocity increases or decreases according to the following equation:

  1. Vt = V0 + a ∙ t

Where:

  • Vt = velocity at time t Vtime
  • V0 = initial velocity
  • a = acceleration
  • t = time

Displacement S is given by the integral of velocity over time, and in
linear motion, it follows the equation:

S=∫Vt dt

  1. S = V0 ∙ t + 1/2 ∙ a ∙ t2

Velocity is also defined as the derivative of displacement:

V= dS/dt

By substituting equation (1) into equation (2) and simplifying, we obtain the third kinematic equation:

  1. Vt2 = V02 + 2 ∙ a ∙ S
  2. "S = V0 + Vt / 2  ∙ t

 

In Cart motion on inclined plane experiment, we measure the motion of a cart on an inclined plane using a motion sensor and examine how the experimental results fit these equations.

 

This hands-on experiment allows students to apply these formulas to real-world data, helping them understand how motion parameters interrelate and how they can be visually represented through graphs. For teachers, this provides an opportunity to guide students in connecting theoretical physics principles with practical observations.